Hindley Milner typechecking by example

So I’ve been getting really interested in typechecking, and well, the best way to learn is to try and explain it in words, so here we go.

There are many kinds of typechecking, but today I want to explain a variation on Hindley Milner (I’ve also seen it called Damas Milner, please feel free to ping with the actual truth, fact fans). This kind of type system is the kind you’ll find under OCaml, Elm, Haskell and Purescript, although each language has their own variations (and in the case of Haskell, a terrifying number of extensions to it).

A working example

We’re going to start by typechecking the simplest stuff, and then build up features as we go. There are three stages to our algorithm, Elaboration, Unification and Substitution. We’ll introduce them as we need them.

🥚 Elaboration 🥚

Here go through the expression we’d like to typecheck, marking each part of the AST with the thing we think it is (and if we don’t know, we sort of guess). We’ll also produce a set of constraints about the types we’ve worked out (a constraint is something like “I don’t know a or b are but I know they’re the same thing”)

Literals

Literals are static values declared in code. Our toy language has the Boolean, Integer and String types. As this means there is no ambiguity between them, we can work out their types in the Elaboration stage alone.

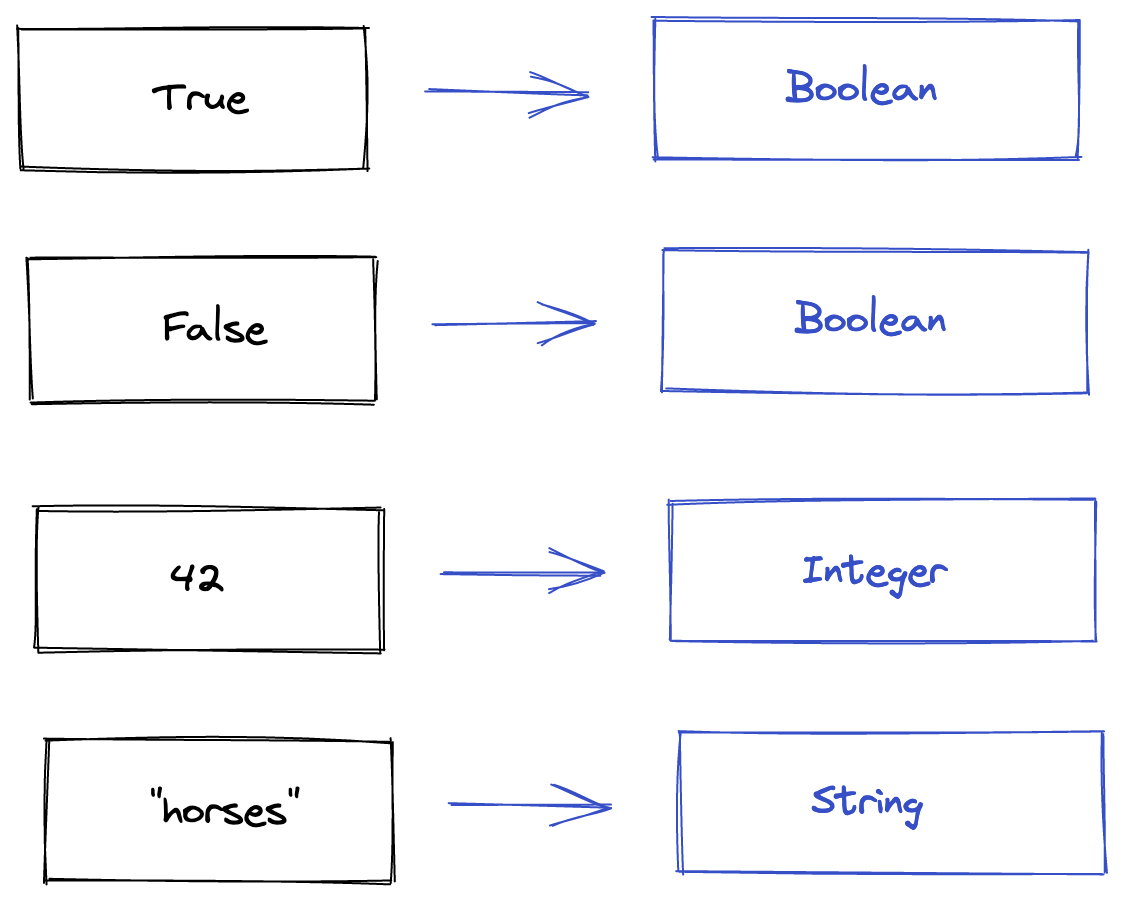
The values are on the left in black, the types on the right in blue. No weird surprises here, hopefully.

Let bindings

It is nice to be able to give things names, so we should have some let bindings in our language. These allow us to introduce a new concept - the typechecking environment. A let binding has two sub-expressions - the first is the one that gets “bound” and assigned to the name, and then the body, which can refer to the bound expression by name.

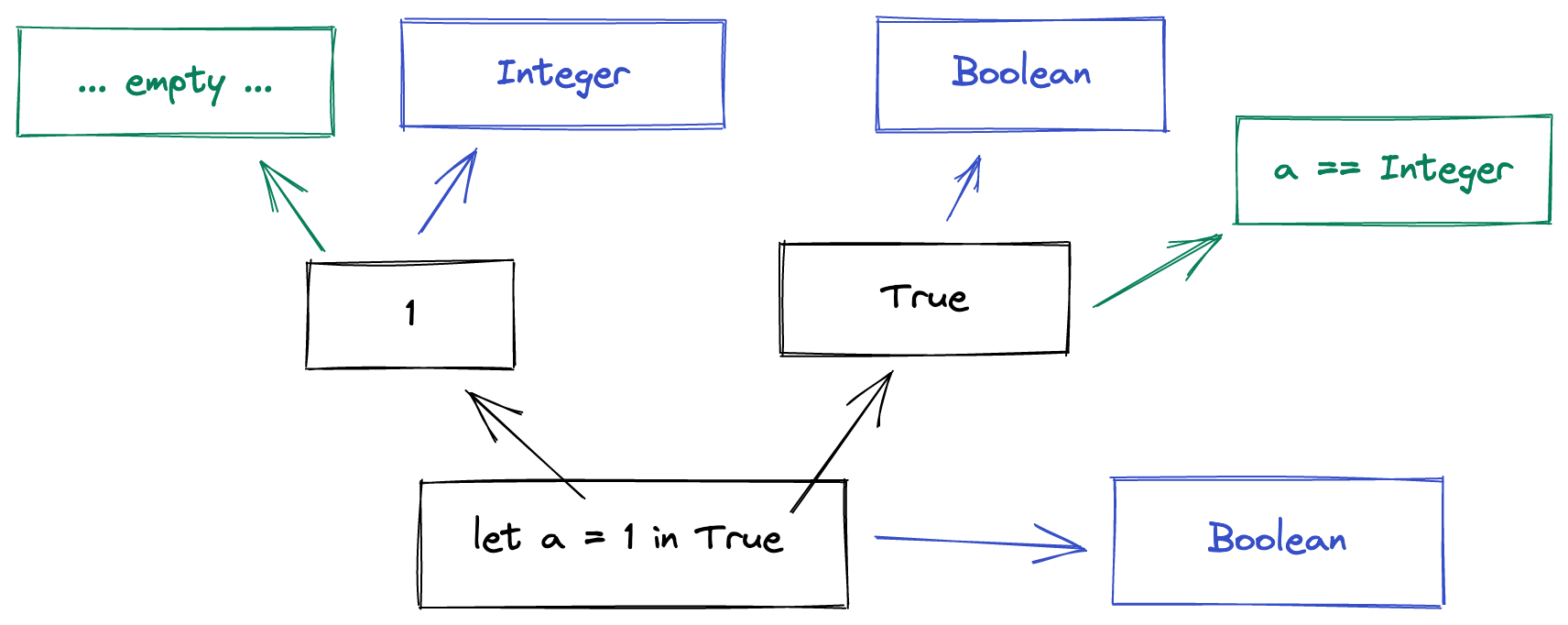
In this example, our environment (shown in green) is initially empty, but as we were able to elaborate the type of a as Integer, the environment when typechecking the body also includes a == Integer. However, this has no effect on the type of the whole expression, as the body of the let binding is True which we know is of type Boolean.

Variable

It’s all well and good making variables, but it’s even more useful to refer to them later. Given a typechecking environment that already knows about b, we can look it up:

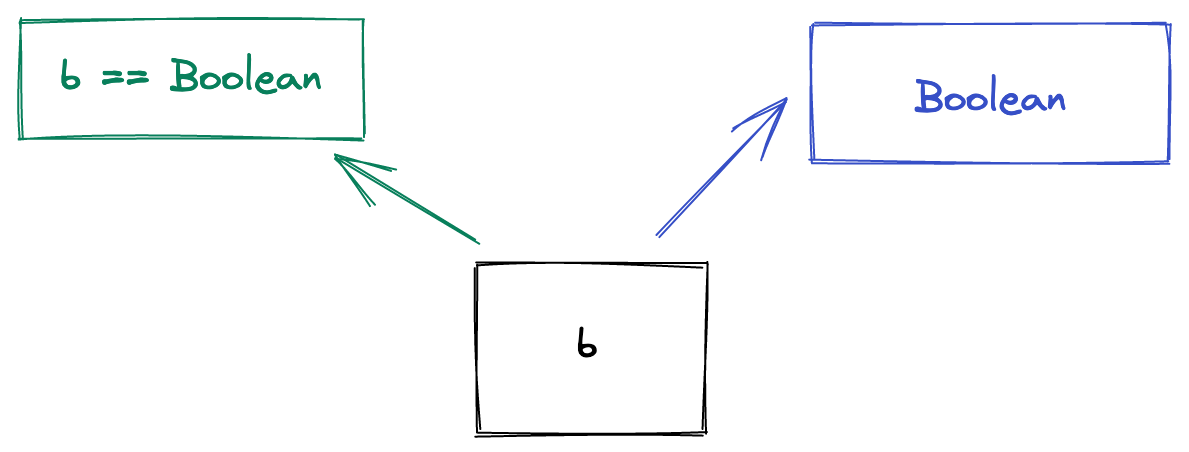
If it’s not there, we throw a type error and tell the user they’ve made a typo or something. If it is, then we return the type from the environment.

If / Then / Else

An if statement in our language is an expression, meaning it must return something from both the then and the else branch. It contains three sub-expressions, one for the predicate we are testing (which must be of type Boolean), one for the then branch, and one for the else branch.

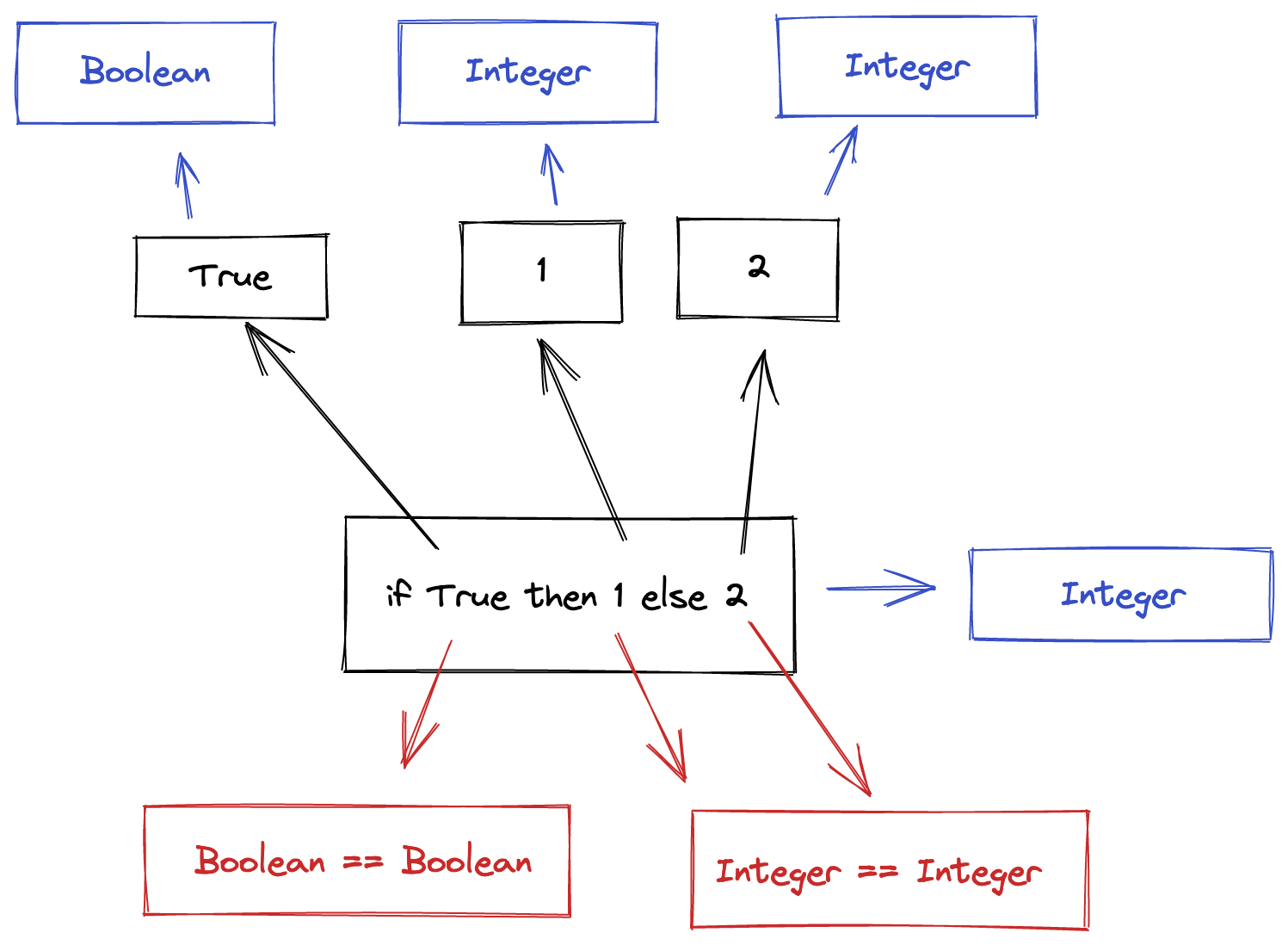
Because each of these sub-expressions are literal values, we can elaborate their values as we did above. The return type is Integer, as that is the type we have worked out for the then branch (it could as well be the type of the else branch, they should be the same).

How do we ensure all our rules work out? That’s the job of the constraints that we have generated (shown in red). We have one that ensures the type of True matches Boolean, and another that ensures the types of the then and else branches are the same.

🥚 Unification 🥚

Now that we have constraints, we need to check they make sense. Unification in the context of typechecking is about smashing two things together and seeing what we learn.

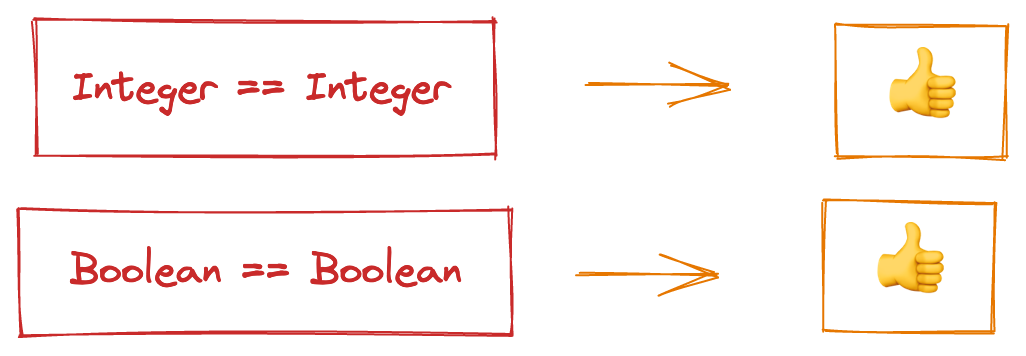
The outcome of unification is either a type error or a set of substitutions, such as “replace all c values with String”.

Here the two things are the same in both cases, so everything is fine and we learn nothing new.

Lambda

A lambda is a function abstraction. When elaborating lambdas, we don’t know what the type of the argument will be. Different type systems have different approaches to this problem. One solution is to make the programmer annotate the argument with a type (ie, \(a: String) -> ...). However, Hindley Milner typechecking is all about minimising type annotations, so instead we’ll guess it. We do this by creating a fresh unknown type variable called a “unification variable”. Each of these should be unique within the typechecking, so they often use numbers with an internal counter to generate fresh ones. We’re going to use the unimaginative unknown-1.

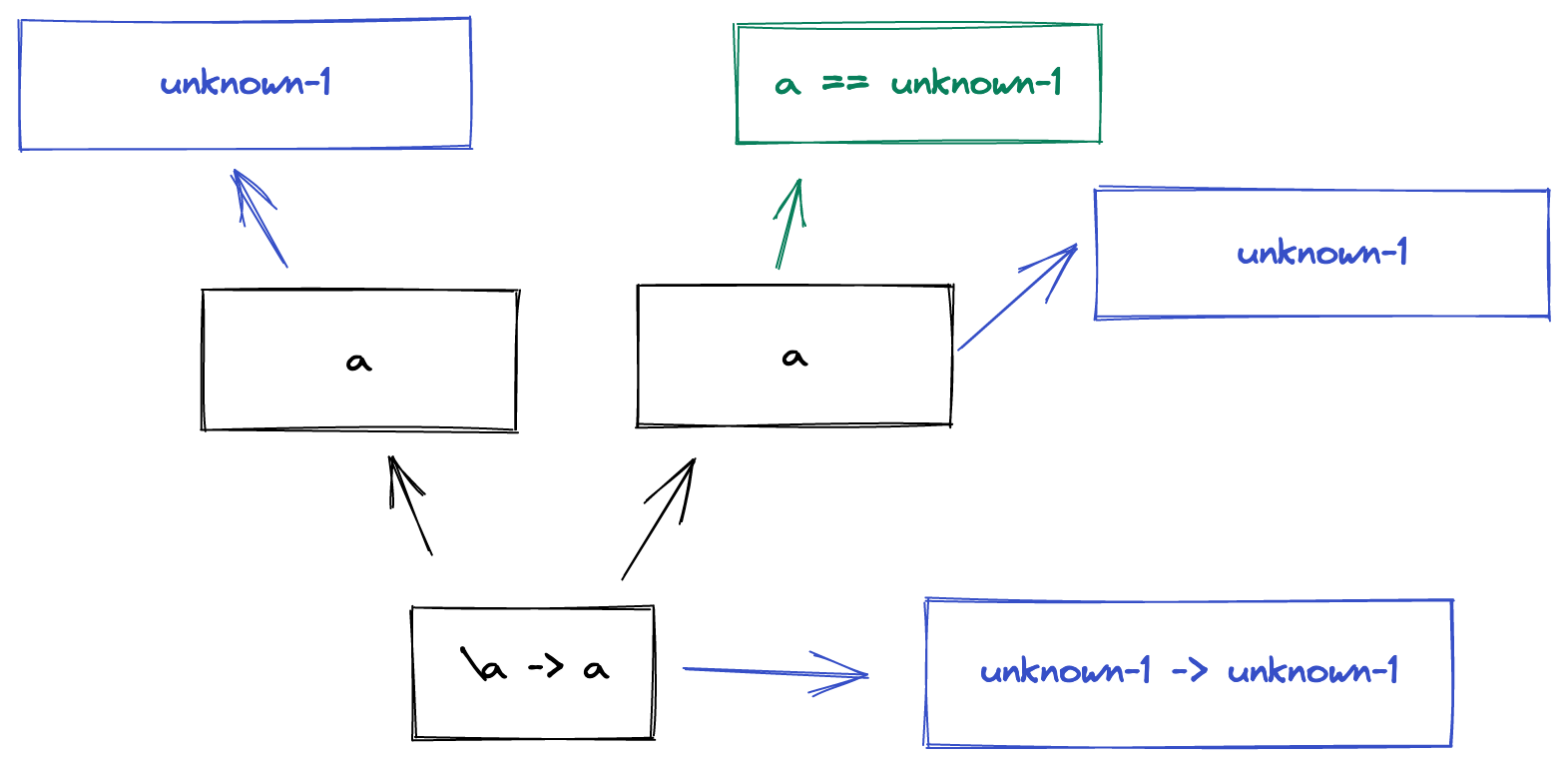
Then, when we elaborate the body of the lambda, we add a == unknown-1 to the environment, which makes typechecking the variable a straightforward, making the type of the whole lambda unknown-1 -> unknown-1 (the -> meaning “a function from a to b”)

Function application

Elaboration

What’s the use in functions if we can’t apply values to them? Given the id function has already been defined, let’s apply a value to it.

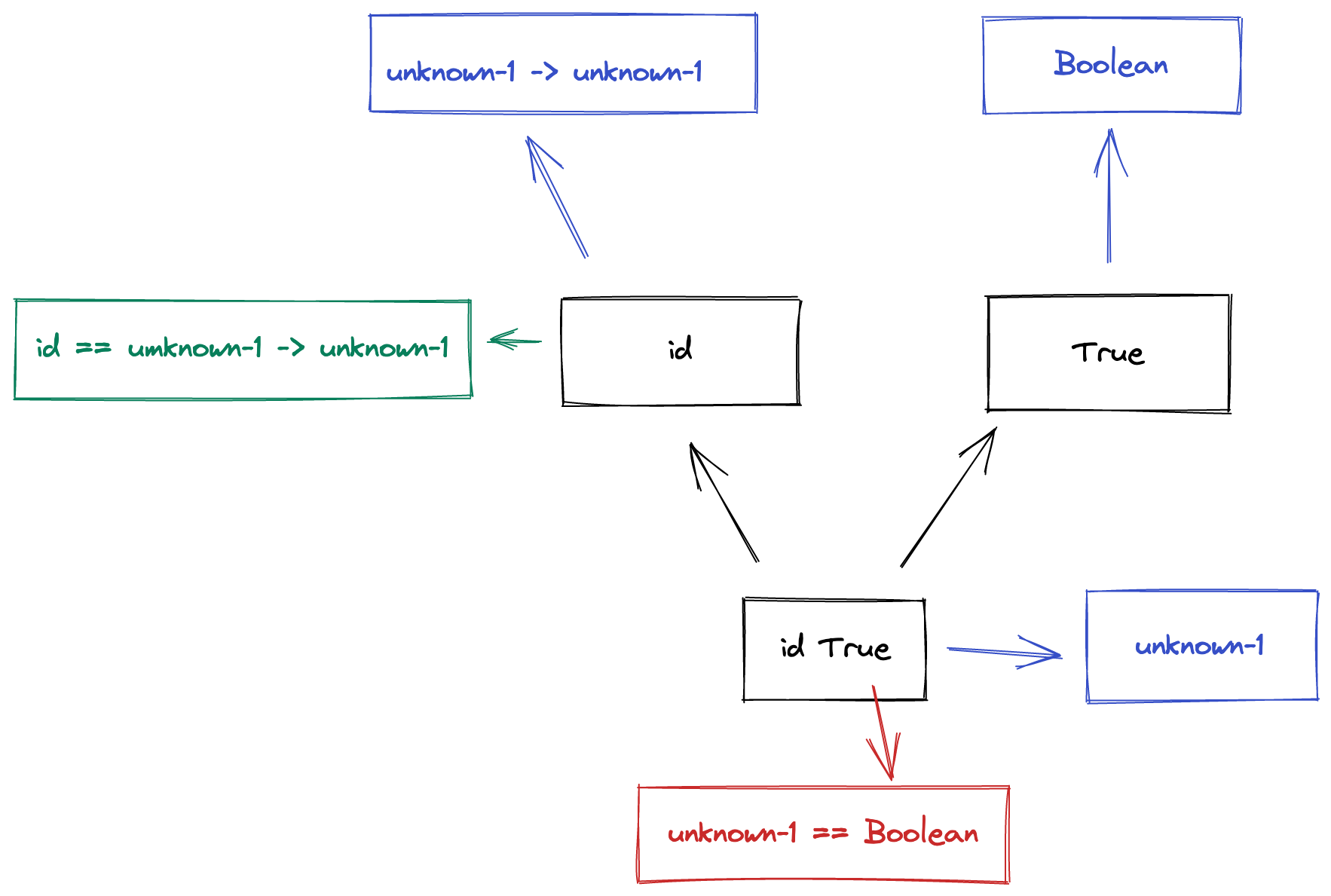
Since the function type is unknown-1 -> unknown-1, we apply Boolean to it, by creating a constraint between the first unknown-1 and Boolean. Then the return type from elaboration is the second half of the function type (also unknown-1).

Surely it should be Boolean though right? No, but also, yes, but also, it’s complicated…

Unifying our new constraint

Let’s look at the constraint we’ve generated during elaboration.

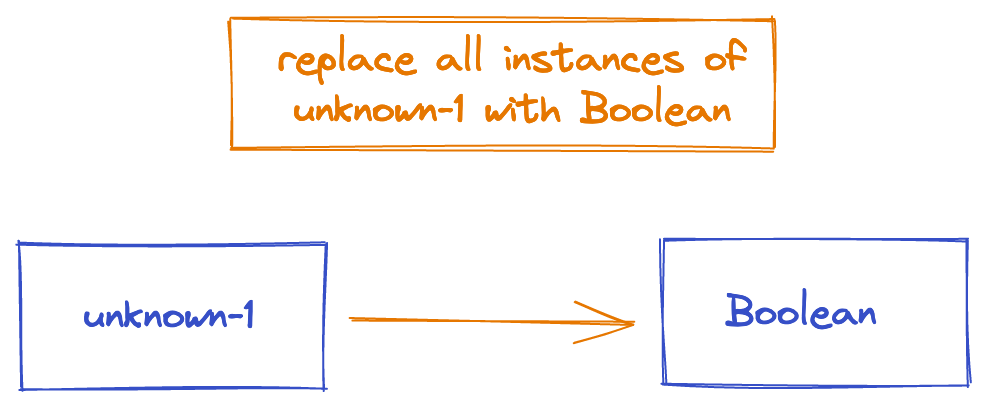
As we briefly mentioned earlier, we unify values to learn things about them. Because unknown-1 is a unification variable, it represents an unknown thing that we are trying to find out more about. Unifying it with Boolean tells us unknown-1 is actually Boolean, and therefore we can substitute any instance of unknown-1 for Boolean.

Apply the substitution

We apply a substitution by changing all instances of one thing in a type for another. Applying a substitution to the result of elaboration gives us our final type, Boolean

🥚 Substitution 🥚

Assuming we had no type errors in the previous step, then subsitution is the process of taking all the things we have learned and applying them to both to expression and to the other substitutions.

For example, if we have learned “a is an Integer” then we can change any a values in our expression to Integer, and also change the substitution “c is a pair of a and b” into “c is a pair of Integer and b”.

A bigger example

To see Hindley Milner typechecking in action, here is a slightly bigger example. Here we’ll see how we can get full type inference without a type annotation in sight.

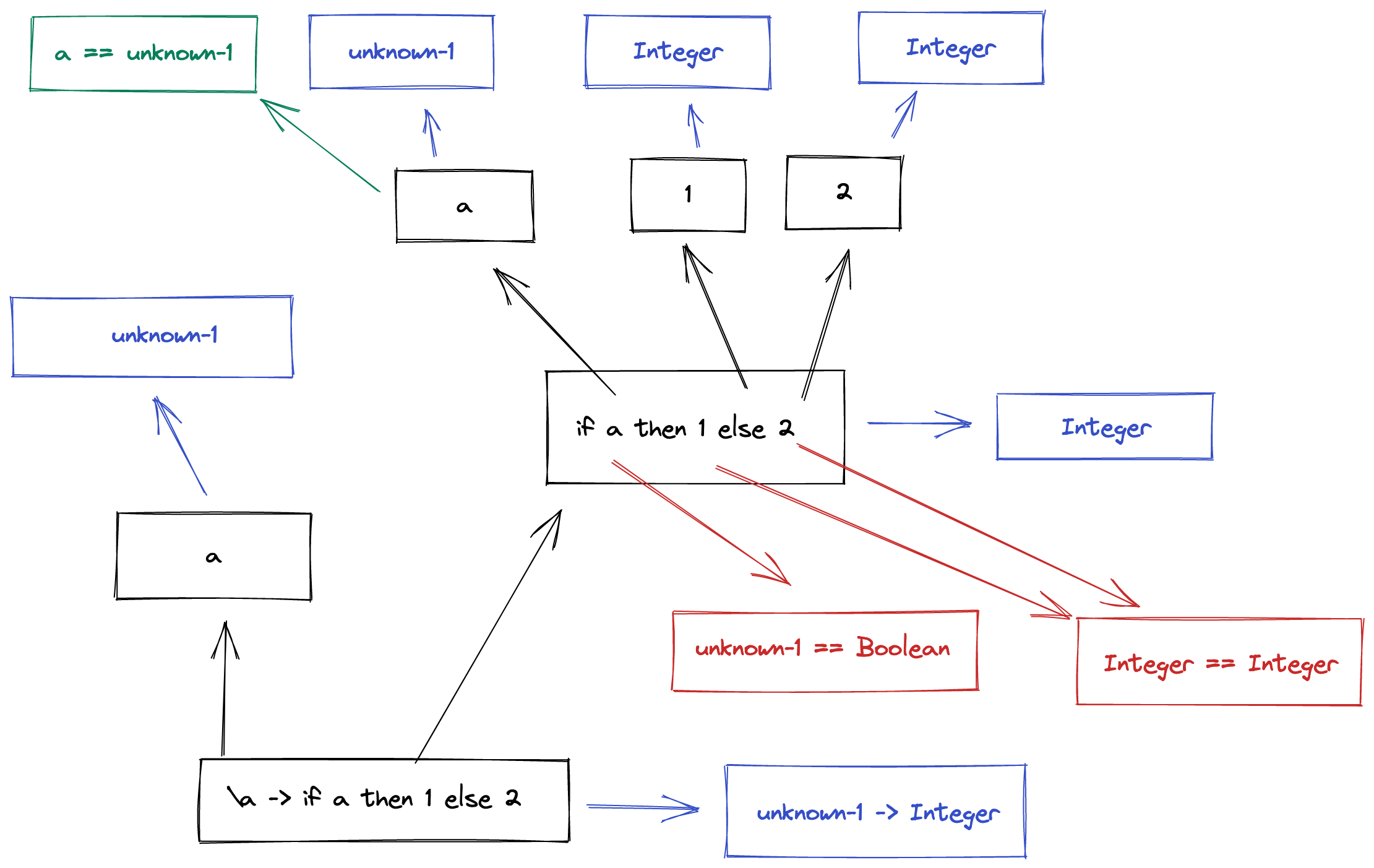
We start by elaborating the function argument, a. We have no idea what it is, so we create a unification variable, unknown-1, and use that instead.

Then we move onto the body of the lambda, an if expression. The predicate expression is a. Fortunately, we already have the type for a in the type environment - so we can grab it. We don’t know what unknown-1 is yet, but we have another piece of information on our side - the predicate for an if must be a Boolean. We express this by creating a new constraint unknown-1 == Boolean.

The then and else expressions are both literals, so we can infer those quite simply, making Integer the return type of the if expression. There is also another constraint here, that both branches should have the same type - Integer == Integer.

Unifying our new constraints

We have two contraints from elaboration.

First Integer == Integer, which teaches us nothing (but does type check).

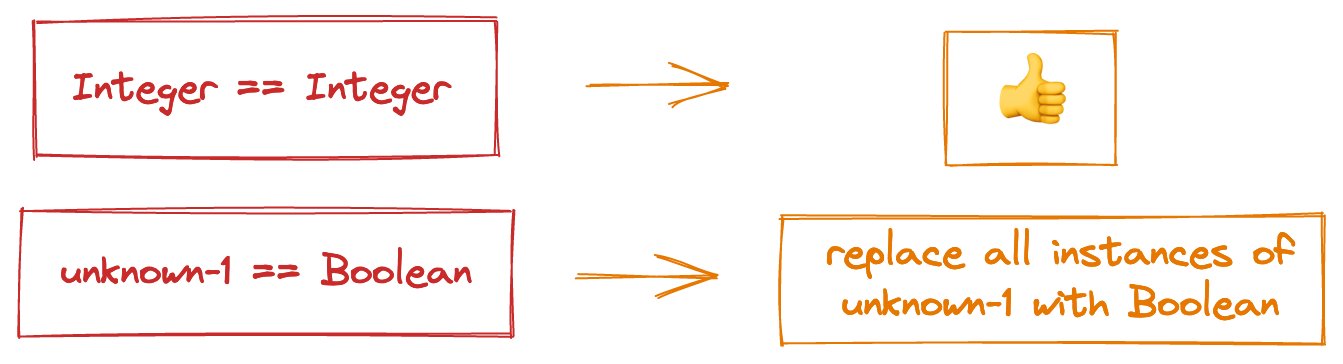
Secondly unknown-1 == Boolean gives us a substitution.

Apply the substitution

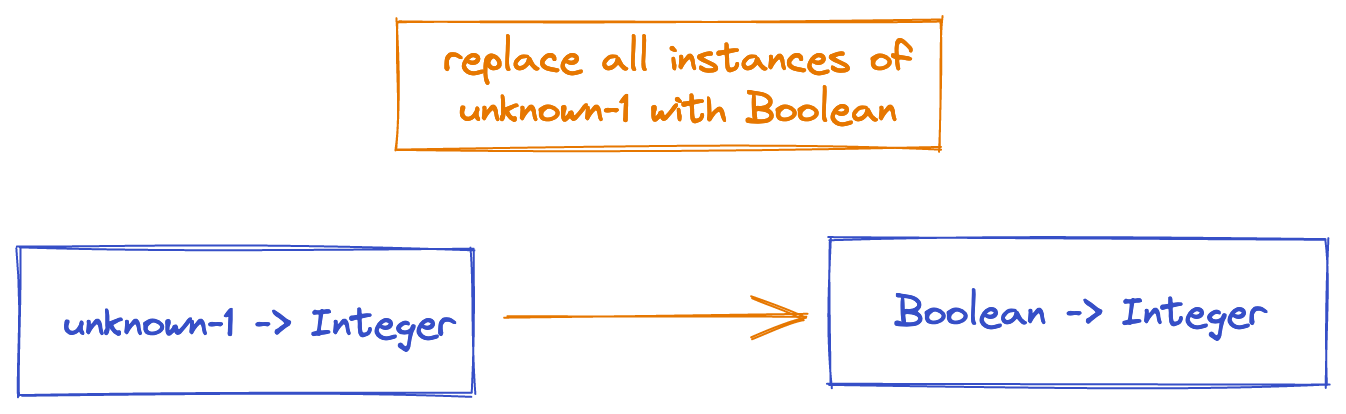
So, therefore, the type of \a -> if a then 1 else 2 is Boolean -> Integer.

That’s all folks

The writing that is, that is the end of the writing. There is a bunch more to Hindley Milner typechecking, we’ve neatly sidestepped any complicated polymorphism, however rest assured that it doesn’t make things too much complicated which is nice. I might write about that in future, so given the glacial pace of my writing, look forward to a sequel in 2024.

Make sense? If not, get in touch!

Further reading:

giml

Write you a Haskell

mimsa